|
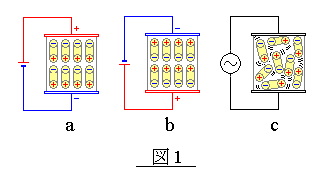
誘電体に電界を印加すると、誘電体内部に持つ電子やイオンなどの荷電体の移動による分極を生じ、
右図a,bのように正負の極性双極子が電界の方向に向きを揃えようとします。 1秒間に何百万回も極性が入れ替わる数〜数100MHzの高周波交流の電界中では、 右図cのように 電界の反転に追従しようとする双極子の激しい運動による摩擦が 発熱を生みだします。 |
 |
| もうすこし電気屋さん的 (^^; に説明しますと・・・ |
 |
Xc = 1/(2πfC) |
|
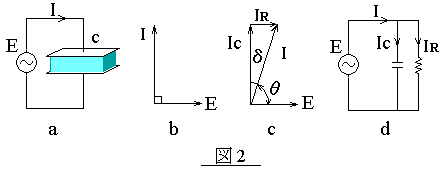
図2-a のように誘電体と1対の電極板で構成されるコンデンサの容量を C とし、このコンデンサに交流電圧 E を印加すると、I = E× 2πfC なる電流が流れ、同-b のベクトル図で示すように電流の位相は電圧に対して90゜進みます。 ところが、周波数が高い高周波交流では誘電体のロスにより δ だけ遅れ、同-c のように 90゜−δ = θ だけしか進みません。 等価回路では同-d のように書き、I は IC と IR のベクトル合成されたものと考える事ができます。このうち電圧E と同位相である IR についてP = IR × E なる発熱作用が発生します。 このδを誘電損失角、tanδ= IR/IC =1/2πfCRを誘電正接といい、誘電体である物質それぞれ固有の値をもっています。 |
図2-a に於いて
とすると、このコンデンサの容量は P=E2/R=E2×tanδ×2πfC=E2×tanδ×2πf×S/d (W) 単位体積当たりの電力を考えると P0=P/(S×d) であるから、 P0=(E2×tanδ×2πf×ε0×εr)/d2 =(E/d)2×tanδ×2πf×ε0×εr =(E/d)2×5.56×10-11×f×εr×tanδ (W/m3) よって発熱に係る単位体積あたりの電力は、電界の強さ(E/d)の2乗、周波数f、比誘電率εr、誘電正接tanδ に比例する、ということになります。 この式は誘電加熱を説明する時にしばしば用いられ、εr×tanδ をロス・ファクタと呼んで加熱しやすさの目安としています。表1は各種物質の比誘電率と誘電正接の例であり 0.01<εr×tanδ<1 程度が良好な誘電加熱の条件とされています。 |
||||||||||||||||||||
| 関連項目 |
| ■高周波誘電加熱の原理 |
| ■高周波誘電加熱の特徴 |
| ■高周波誘電加熱装置の構成例 |
| ■高周波誘電加熱の応用例 |
| ■EMC問題について |
| ■関連法規等 |
| ■弊社装置の故障・修理に関する技術資料 |
| ■故障・修理に関するお問い合わせ |
© Fuji Electronic Ind. Co. All rights reserved.